--- ### Constant Product Formula Explained In order to get started writing our fuzzing test suite we'll need to define what TSwap's core invariant is. Fortunately the protocol provides this in their README. ```md Our system works because the ratio of Token A & WETH will always stay the same. Well, for the most part. Since we add fees, our invariant technically increases. x \* y = k x = Token Balance X y = Token Balance Y k = The constant ratio between X & Y y = Token Balance Y x = Token Balance X x _ y = k x _ y = (x + ∆x) \* (y − ∆y) ∆x = Change of token balance X ∆y = Change of token balance Y β = (∆y / y) α = (∆x / x) Final invariant equation without fees: ∆x = (β/(1-β)) _ x ∆y = (α/(1+α)) _ y Invariant with fees ρ = fee (between 0 & 1, aka a percentage) γ = (1 - p) (pronounced gamma) ∆x = (β/(1-β)) _ (1/γ) _ x ∆y = (αγ/1+αγ) \* y ``` This may look confusing at first, and that's ok. This is known as the `constant product formula` which effectively states: **The PRODUCT should always be the same - x\*y should always equal the same k** We should pay special mind to this line in our documentation however: ``` Since we add fees, our invariant technically increases. ``` With that said, this is definitely an invariant we can test. The ratio between tokens x and y should always remain the same `x * y = (x + ∆x) * (y − ∆y)`. Remember back to `How an AMM works`. 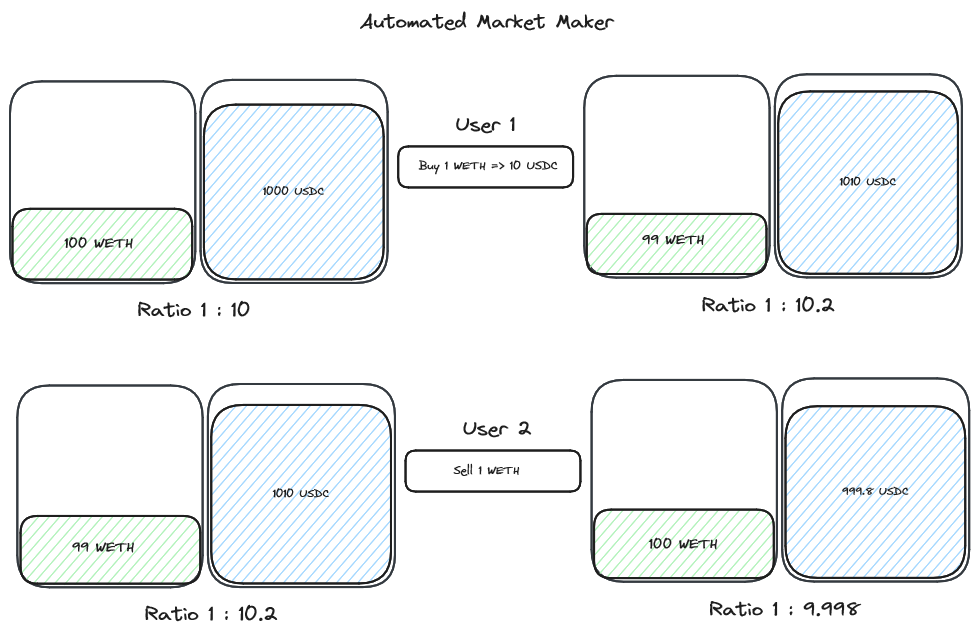 Writing an assert for `x * y = (x + ∆x) * (y − ∆y)` can be difficult, but what we can do is write one that defines that any change in token balance must follow some formula. We can actually see this equation in the core invariant documentation we've been provided: ``` Final invariant equation without fees: ∆x = (β/(1-β)) * x ∆y = (α/(1+α)) * y ``` We're going to use some algebra to derive this equation for our tests then write a stateful fuzz test suite. Don't worry too much if you don't understand all the math straight away. ### The Math Let's go through the math to understand how we derive this invariant. We begin with this formula: 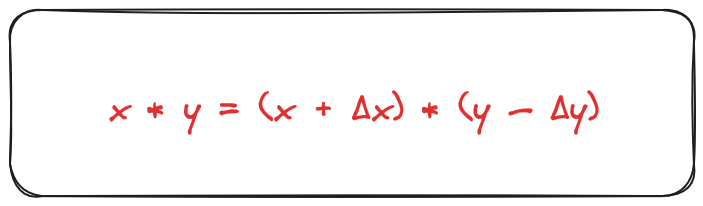 We should be able to leverage some basic algebra to get where we need. First we're going to apply the concept of FOIL (First Outside Inside Last) to multiply our binomials. 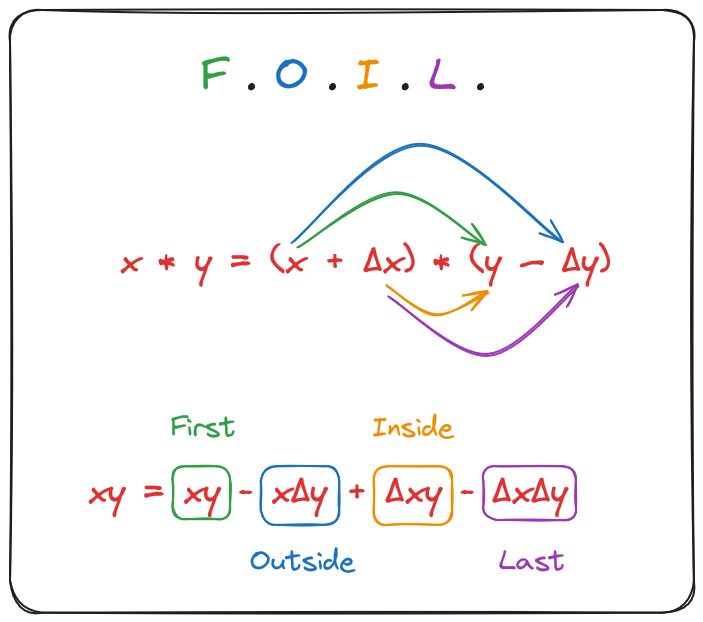 Next the equation will need to be simplified with the following steps.  In the next step we're going to introduce a new term `β` and define it as `∆y/y`. Which will allow us to simplify things further.  And that's it, we can go back to the TSwap documentation to confirm: `∆x = (β/(1-β)) * x` ### Wrap Up Whew! Hope you enjoyed this math filled deep dive into the constant product formula. In the next lesson we're going to start writing `Invariant.t.sol` for TSwap. I can hardly wait - see you there!
Constant Product Formula Explained
In order to get started writing our fuzzing test suite we'll need to define what TSwap's core invariant is. Fortunately the protocol provides this in their README.
This may look confusing at first, and that's ok. This is known as the constant product formula which effectively states:
The PRODUCT should always be the same - x*y should always equal the same k
We should pay special mind to this line in our documentation however:
With that said, this is definitely an invariant we can test. The ratio between tokens x and y should always remain the same x * y = (x + ∆x) * (y − ∆y).
Remember back to How an AMM works.

Writing an assert for x * y = (x + ∆x) * (y − ∆y) can be difficult, but what we can do is write one that defines that any change in token balance must follow some formula.
We can actually see this equation in the core invariant documentation we've been provided:
We're going to use some algebra to derive this equation for our tests then write a stateful fuzz test suite. Don't worry too much if you don't understand all the math straight away.
The Math
Let's go through the math to understand how we derive this invariant.
We begin with this formula:
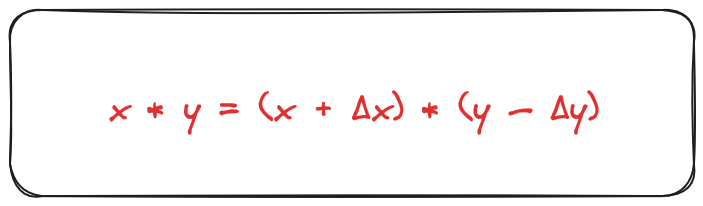
We should be able to leverage some basic algebra to get where we need. First we're going to apply the concept of FOIL (First Outside Inside Last) to multiply our binomials.

Next the equation will need to be simplified with the following steps.

In the next step we're going to introduce a new term β and define it as ∆y/y. Which will allow us to simplify things further.

And that's it, we can go back to the TSwap documentation to confirm: ∆x = (β/(1-β)) * x
Wrap Up
Whew!
Hope you enjoyed this math filled deep dive into the constant product formula. In the next lesson we're going to start writing Invariant.t.sol for TSwap. I can hardly wait - see you there!
Constant Product Formula Explained
Explore the constant product formula and test it's implementation in TSwap through Fuzz and Unit testing.
Previous lesson
Previous
Next lesson
Next
Duration: 25min
Duration: 1h 30min
Duration: 35min
Duration: 2h 28min
Duration: 5h 04min
Duration: 5h 23min
Duration: 4h 33min
Duration: 2h 01min
Duration: 1h 41min